Eine Sinusschwingung ist die reinste aller Schwingungen. Wir nutzen das in der Funktechnik, um in der Frequenz benachbarte Sinusschwingungen mit Informationen zu belegen und so zu übertragen. Wir sagen, solch eine Übertragung belegt eine Bandbreite benachbarter Frequenzen. Damit das funktioniert, müssen die elektrischen Signale linear verarbeitet werden. Tut man das nicht, entstehen Harmonische. Das sind Vielfache der Grundfrequenz der gewünschten Schwingungen. Damit diese unerwünschten Harmonischen nicht abgestrahlt werden, müssen Sie mit Tiefpassfiltern wieder unterdrückt werden.
In dem Zusammenhang werden die Begriffe Schwingungen und Wellen oft synonym verwendet. Es gibt aber einen klaren Unterschied: Solange die Frequenz nur lokal existiert, also beispielsweise in der Elektronik eines Senders, handelt es sich um eine Schwingung. Wenn sie über die Antenne abgestrahlt wird und sich in Raum und Zeit ausbreitet, handelt es sich um eine Welle. Mehr dazu hier.
Die Fourier-Transformation gibt uns die Möglichkeit zu berechnen, wie Signalform und Harmonische zusammen hängen. Dazu brauchen wir nicht die vollständige Mathematik von Fourier. Diese wird z. B. genutzt, um in SDR ein komplettes Band darzustellen und ermöglicht das sogenannte Wasserfall-Diagramm.
Hier reicht uns die einfachere Reihenentwicklung nach Fourier. Aber auch für die benötigt man immer noch Integralrechnung. Aber auch die muss man nicht selbst machen. Es gibt sogenannte Algebra-Software, die das für einen erledigt. Ein schönes Tool im Internet dafür ist Wolfram Alpha. Man benötigt also eine mathematische Beschreibung für die Kurvenform, die man betrachten möchte.
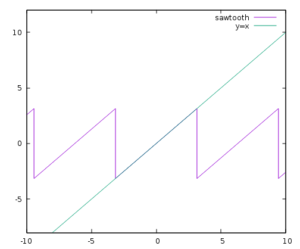 Der Sägezahn lässt sich innerhalb einer Periode einfach durch y=x beschreiben. Dann setzt man diese Funktion in die Reihenentwicklung ein und erhält die Funktion, die man integrieren muss:
Der Sägezahn lässt sich innerhalb einer Periode einfach durch y=x beschreiben. Dann setzt man diese Funktion in die Reihenentwicklung ein und erhält die Funktion, die man integrieren muss:
x sin(kx)
Nun fragen wir also Wolfram Alpha nach:
assuming k is an integer, integrate x sin(k*x) from 0 to 2 * pi
Hier ist das Ganze dann ausformuliert: fouriersägezahn .
Wir erhalten also das vermutlich schon bekannte Ergebnis, dass der Sägezahn alle Harmonischen einer negativen Sinusschwingung mit um 1/k fallender Amplitude und gleicher Phasenlage im Nullpunkt enthält. Die Phasenlage interessiert uns zwar in der Funktechnik eher selten, aber nur wenn man sie berücksichtigt, erhält man grafisch das richtige Ergebnis.
Um solche Funktionen grafisch darzustellen, kann man Wolfram Alpha bemühen, aber es geht z. B. auch offline mit GnuPlot.
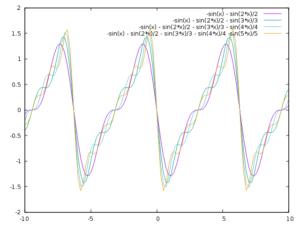
GnuPlot erlaubt einfach Komma-separiert mehrere Funktionen in der gleichen Grafik darzustellen. Um sich also anzuzeigen, wie aus einem Sinus durch Hinzufügen der Harmonischen allmählich ein Sägezahn wird, kann man Folgendes in GnuPlot eingeben:
plot \ -sin(x) - sin(2*x)/2, \ -sin(x) - sin(2*x)/2 - sin(3*x)/3, \ -sin(x) - sin(2*x)/2 - sin(3*x)/3 - sin(4*x)/4, \ -sin(x) - sin(2*x)/2 - sin(3*x)/3 - sin(4*x)/4 - sin(5*x)/5
Und dann erhält man Ergebnis so eine Grafik:
Man sieht deutlich, dass der fallende Ast immer steiler wird und die Spitzen immer ausgeprägter werden, mit immer mehr Harmonischen. Der steigende Ast hingegen bleibt wellig und wird erst mit viel mehr Harmonischen gerade.
Genauso wie den Sägezahn kann man auch das Dreieck als Signalform nach Fourier analysieren. Wer mag, kann das selbst für ein symmetrisches Rechteck durchrechnen. Bei sinnvoller Wahl des Rechtecks im Koordinatensystem ist es einfacher als das Dreieck, weil man keine bereichsweise Definition benötigt. Am Ende sollte herauskommen, dass die Amplituden der ungeraden Harmonischen mit 1/k fallen.
Im Artikel über den Eichmarkengeber wird der aufwändigere Fall eines schmalen Rechtecks behandelt.
Zusammenfassung
Hier noch einmal die Schritte zur Vorgehensweise:
- beschreibe die Kurve als Formel
- vorzugsweise „geschlossen“, also nicht abschnittsweise → weniger Rechenaufwand
- vorzugsweise entweder Punkt-symmetrisch zum Nullpunkt oder spiegelbildlich zur y-Achse → es reicht dann eine Reihe: entweder nur Sinus oder nur Kosinus
- integriere die Funktionen der Reihenentwicklung, ggf. mit einem Algebra-Tool
- vereinfache das Ergebnis unter Berücksichtigung der Rechenregeln für Sinus und Kosinus
- nötigenfalls kann man auch Näherungen verwenden
- kontrolliere das Ergebnis grafisch
Ein Fehler, der leicht passiert ist, dass die Amplituden-Faktoren (hier oft 1/k) im Ergebnis der falschen Funktion zugeordnet werden. Es gilt immer die Funktion noch vor dem Integrieren!
Und nicht wundern, wenn das eigene Ergebnis von denen „im Web“ abweicht. Sinus und Kosinus sind sich halt sehr ähnlich und lassen sich ineinander auf verschiedene Weisen umrechnen. So ergeben sich viele Darstellungen, die gleichermaßen korrekt sind.
Zählweise
Die mathematisch natürliche Zählweise wird Harmonische genannt. Hier ist die Null auch die Null der Frequenz und die 1 entspricht der Grundschwingung. Wie man oben bei der Befehlszeile für Gnuplot sieht, lässt sich diese Zählung direkt in die Formel übertragen. In der Technik spricht man auch gern von Oberschwingungen. Deren Zählung ist um 1 versetzt. Die 2. Harmonische ist also die erste Oberschwingung. Die Grundschwingung entspricht hier also der Null. Falls es hier Missverständnisse geben kann, sollte genau definiert werden, welche Zählweise gelten soll. Hier eine Grafik zur Veranschaulichung mit 3,6 MHz als Beispiel für eine Grundschwingung.