Differentialrechnung

Viele Dinge im Amateurfunk sind mit dem hier angebotenen Rechenkurs nicht wirklich zu verstehen. Andererseits kann dieses Blog auch mehrere Jahre Schulmathematik oder gar Studium nicht ersetzen. Aber ich will versuchen, in einfachen Worten ein paar Dinge zu erklären. Das hilft vielleicht beim Verständnis bei Themen wie „differenzieller Widerstand“, „über die Zeit integriert“ bis hin zur Fourier-Transformation.

Ableitung

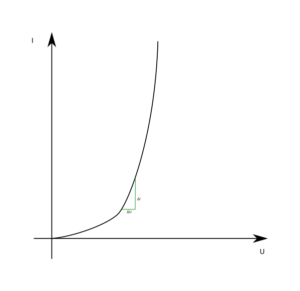Betrachtet man an einer Kennlinie eines Bauteils den differenziellen Widerstand, so stellt man sich das meist als Steigungsdreieck vor. Man berechnet den Widerstand an dieser Stelle, in dem man das ΔU durch ΔI teilt:

R_diff = ΔU / ΔI

Das Bauteil verhält sich also an dieser Stelle in der Kennlinie wie ein Widerstand mit R=R_diff. Dabei bleibt immer ein kleiner Fehler, weil man den Kurvenverlauf innerhalb des Dreiecks als Gerade annimmt. Um das zu vermeiden, macht man das Steigungsdreieck möglichst klein.

Nun kann man einen sogenannten Grenzübergang machen. Man verkleinert das Steigungsdreieck immer weiter. Am Ende betrachtet man nicht mehr ein Steigungsdreieck, sondern legt an die Kennlinie eine Tangente und bestimmt deren Steigung. Diese Steigung stimmt mathematisch exakt für den Punkt an der Tangente. Macht man das für jeden Punkt der Kennlinie, erhält man die sogenannte Ableitung der Kurve. Um in der Schreibweise deutlich zu machen, dass man nicht mit einem Steigungsdreieck an der Kurve, sondern mit einem an der Tangente gerechnet hat, benutzt man anstelle des großen griechischen Buchstabens Delta Δ das kleine d als Ableitungssymbol:

R_diff = dU / dI

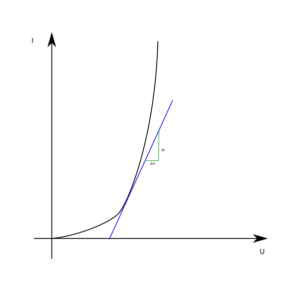Die Ableitung der Kurve beschreibt also in jedem Punkt die Steigung der Kurve. Diese Art, mit den kleiner werdenden Differenzen am Steigungsdreieck umzugehen, nennt man Differenzialrechnung. Das ist nicht zu verwechseln mit den Differenzialgleichungen DGL. Letztere beschreiben, wie man mit den Differenzialen rechnet. Das werden wir hier nicht behandeln.

In der Elektrotechnik ist die Ableitung der I/U-Kennlinie der differenzielle Widerstand des Bauteils.

Integral

Betrachtet man den Leistungsbedarfs P eines Geräts über der Zeit t, so kann der Energieverbrauch E berechnet werden, in dem man die Leistung mit der Zeit multipliziert, also:

E = P * t

Grafisch bedeutet das, wir berechnen die Fläche von einem Rechteck mit Kantenlängen P und t. Das geht nicht mehr so einfach, wenn sich die Leistung mit der Zeit ändert. Man kann einen ähnlichen Trick wie bei der Ableitung machen: Wir betrachten nicht die Kurve selbst, sondern ein anderes Konstrukt, welches wir einfacher beschreiben können: Man zerteilt die Kurve in schmale Rechtecke, die jeweils an ihrer Position im Mittel die richtige Höhe haben und summiert diese Rechtecke auf.

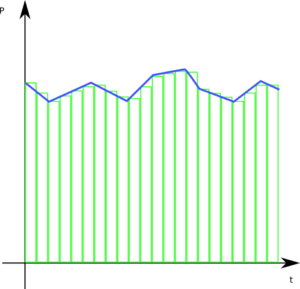Nun macht man wieder einen sogenannten Grenzübergang und macht die Rechtecke immer schmaler. Dadurch passen sie sich immer besser der Kurve an. Hier ist es etwas schwieriger zu verstehen, wie das genau funktioniert, denn am Ende hat man unendlich viele unendlich schmale Rechtecke, also nur noch Linien.

Man sagt, um die Energie zu erhalten, muss man die Leistung über die Zeit integrieren. Das exakt zu beschreiben, würde zu weit führen. Wir merken uns hier, dass man die Fläche unter einer Kurve Integral nennt und diese ggf. per Software berechnet werden kann. Um hier deutlich zu machen, dass man nicht einfach eine Leistung P mit der Zeit t malgenommen hat, sondern dass hier zu jedem Zeitpunkt die richtige Leistung aufsummiert wurde, benutzt man diese Schreibweise:

$$ E = \int{P dt} $$

In der Elektrotechnik ist das Integral der P/t-Kurve der Energieverbrauch eines Geräts.

Transformation nach Fourier

Im Empfänger kommen Signale von vielen Frequenzen über die Zeit in wechselnden Signalstärken an. Möchte man das grafisch darstellen, kann man ein Sägezahnsignal auf den VCO eines Empfängers geben. Den Sägezahn gibt man auf den x-Eingang eines Oszilloskop und die y-Achse zeigt die Signalstärke an. Auf einer gegebenen ZF-Bandbreite funktioniert das ganz gut und das wurde auch lange so gemacht.

Aber auch hier gibt es die Variante, das mit Software zu machen. Nach Fourier gibt es einen mathematischen Zusammenhang zwischen der Signalstärke über der Zeit und der Amplitude über der Frequenz. Dieser Zusammenhang steckt im Integral. Das Integral der Leistung über der Zeit entspricht dem Integral der Energie über der Frequenz.

Durch die Transformation wird die originale Funktion gewissermaßen auf jede mögliche Frequenz abgetastet, um den Pegel und die Phasenlage bei dieser Frequenz zu ermitteln. Das nun genau mit Worten zu beschreiben führt hier zu weit. Aber hier gibt es ein recht anschauliches Video, welches diese Abtastung schön veranschaulicht:

Youtube

Das könnte man für eine Funktion exakt ausrechnen. Das Signal liegt aber nicht als Funktion vor, sondern als Messwerte. Man kann die Transformation auch „diskret“ mit Messwerten durchführen. Macht man das mit der originalen Methode von Fourier, wird es sehr kompliziert und Rechenzeit-intensiv.

Es gibt aber eine Variante der Fourier-Transformation speziell für diskrete Messwerte. Mit der Fast Fourier Transformation FFT kann man die Darstellung über der Frequenz schnell und genau berechnen. Diese FFT steht heute als Bibliothek für praktisch jede Programmiersprache und jede Plattform zur Verfügung. Dazu ist sie als Funktion in Software für Bild- und Ton-Verarbeitung vorhanden. Der Programmierer ist hier praktisch „Anwender“ und muss letztlich nicht viel darüber wissen, wie es gemacht wird, auch wenn es sicher nicht schaden kann wenigstens eine Idee davon zu haben.

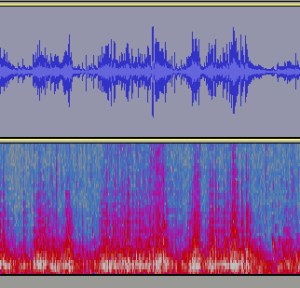Da Rechenleistung heutzutage billiger ist als Analogtechnik, lässt sich mithilfe der FFT eine Spektraldarstellung viel einfacher und universeller durchführen als die Variante mit dem VCO und dem Sägezahn. Gleichzeitig ist mit der Berechnung auch die informativere Darstellung als „Wasserfall“ sehr einfach möglich.

Besonders beim Wasserfall muss man sich über die Achsen klar werden. Da hier auch wieder die Zeit als Achse benötigt wird, um die zeitliche Änderung der Frequenzdarstellung aufzuzeigen, bedient man sich eines weiteren Tricks: Der Pegel wird nicht als Achse dargestellt, sondern als Farbskala. Hier als Beispiel die Darstellung eines Audiopegels und eines sogenannten Spektrogramm aus dem Audio-Tool Audacity.  Niedrige Pegel sind dunkel und blau, hohe Pegel rot und hell.

In der Funktechnik ist die Fourier-Transformation der Wechsel von der Darstellung über die Zeit in die Darstellung über die Frequenz.