Heutzutage will man alles digital haben. Das vereinfacht die Verarbeitung, die Übertragung, die Kompression und Speicherung, digital ist einfach toll. Für die Öffentlichkeit angefangen hat es wohl so richtig damals in den 80er-Jahren mit der Audio-CD. Als interessierter Anwender wusste man, dass die Information darauf mit 16 Bit gespeichert wird. Das reicht theoretisch für 96dB Dynamik, ein fantastischer Wert.
$$ 20 * log_{10} \ 2^{16} = 96 $$
Warum wird hier mit 20 multipliziert? Die Bits definieren einen Spannungswert, die Dynamik wird aber auf die Leistung bezogen. Wie auch von den dBµV bekannt, muss hier also zusätzlich mit 2 multipliziert werden.
Und die Information wird mit gut 40kHz abgetastet. Warum nun mit 40kHz? Das ist doppelt so viel, wie man für HiFi benötigt. Selbst diese 20kHz hören nur die wenigsten erwachsenen Menschen, also eigentlich genug. Warum also gerade doppelt so viel?
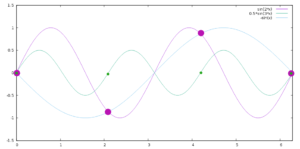Das ist kein Zufall. Betrachtet man nur die einzelnen Abtastpunkte, wenn man z. B. einen Ton von 20kHz nur mit nur 30kHz abtastet, so ergibt die naheliegende Kurve durch die Abtastpunkte eben nicht 20kHz, sondern eine viel niedrigere Frequenz. Dazu verfolgt man in der Grafik die Kurve mit der höchsten Frequenz (grün) und betrachtet immer die Punkte mit dem ansteigenden Nulldurchgang. Es ergibt sich die Kurve mit der niedrigsten Frequenz (blau). Das bedeutet, die Digitalisierung entspricht nicht mehr dem ursprünglichen Signal (lila). Die Theorie dahinter nennt man Abtasttheorem.
Natürlich könnte man auch die „richtige“ höhere Frequenz durch die Abtastpunkte legen. Aber der entscheidende Punkt ist, dass es nicht eindeutig ist. Und da man umgekehrt beim „Abspielen“ der digitalen Daten, also nach dem D/A-Wandler, einen Tiefpass benötigt, um die Abstufungen zu glätten, wird die niedrigste Möglichkeit „gewinnen“. Andersherum gesagt: Die lila und die blaue Kurve hätten die gleiche Abtastung und könnten hinterher nicht mehr unterschieden werden.
Man könnte auch vermuten, dass diese Artefakte nur bei bestimmten Frequenzen passieren. Wer mag kann auch andere Frequenzverhältnisse und Phasenlagen mit Gnuplot oder von Hand durchprobieren. Es wird immer funktionieren, wenn die Abtastfrequenz mehr als doppelt so hoch ist wie die Signalfrequenz und es wird immer diese Artefakte geben, wenn sie zu niedrig ist.
Was bedeutet das nun in der Technik? Jeder Signalanteil, dessen Frequenz höher ist, als die halbe Abtastfrequenz wird uns Störungen, sogenannte Artefakte, in die digitalisierten Daten einbringen. Das kann die Daten gänzlich unbrauchbar machen. Man muss also verhindern, dass zu hohe Frequenzanteile digitalisiert werden. Das macht man naheliegenderweise mit einem Tiefpassfilter.
Das gilt für jede Digitalisierung. Wenn also z. B. ein einfaches SDR für Kurzwelle keine sinnvollen Signale liefert, könnte es genau daran liegen, dass ein UKW-Sender am Eingang des A/D-Wandlers anliegt. Wichtig ist dabei zu verstehen, dass es sich hier nicht um eine Übersteuerung im klassischen Sinne handelt. Schon ein Signal mit einem „normalen“ Pegel verursacht diese Artefakte, wenn es nur auf der „falschen“ Frequenz liegt, die der AD-Wandler nicht verarbeiten kann.
Zu jeder Digitalisierung gehört ein Tiefpassfilter mit der halben Abtastfrequenz.
Ergänzend kann man noch dazu sagen, dass das alles unter der Annahme gilt, dass man alle Frequenzen ab 0 digitalisieren möchte. Verallgemeinernd stimmt genauer, dass die Abtastfrequenz doppelt so hoch sein muss wie die zu digitalisierende Bandbreite. Man könnte also z. B. das 2m-Band mit 4MHz digitalisieren, wenn man sicherstellt, dass auch wirklich nur das 2m-Band auf den Eingang kommt. Anschaulich wird das klar, wenn man sich überlegt, dass es vom Informationsgehalt her keinen Unterschied macht, wenn man das 2m-Band zuerst um 144MHz herunter mischt.
Hier noch ein Beispiel für GnuPlot zum selbst ausprobieren:
plot sin(2.3*x+.5), -sin(.7*x-.5), 0.5*sin(3*x)
