Der Praktiker sagt gern: “Wer viel misst, misst viel Mist”. Betrachten wir hier das zu Grunde liegende Problem etwas theoretischer.
Bringen viele Daten auch viel Erkenntnis? Das hängt davon ab, wie man mit diesen Daten umgeht. Stellen wir uns vor, die unabhängigen Arten von Daten, die wir haben, sind jeweils auf einer Skala. Man kann dann auch sagen, sie stellen eine Dimension dar. Viel Information bedeutet dann, man hat viele Dimensionen. Wenn wir dies versuchen, zusammen darzustellen, erhalten wir einen multidimensionalen Würfel oder einen Hyperkubus. Man kann bei n Dimensionen auch n-dimensionaler Raum sagen.
Um die Informationen nun „als Ganzes“ betrachten zu können, stellt man sich vor, dass wir ausgehend von einem Punkt in diesem Raum die Entfernungen und die Richtungen betrachten. Wir gehen hier davon aus, dass die Auswertung der Daten darauf beruht, dass wir die Datenpunkte auf ähnliche Koordinaten hin untersuchen; genau das ist ihre Entfernung bzw. ihr Abstand zueinander. Das ergibt aber nur Sinn, wenn wir zu allen Richtungen auch den gleichen Umfang an Entfernungen betrachten können. Stellen wir uns auch das geometrisch vor, erhalten wir eine multidimensionale Kugel in unserem multidimensionalen Würfel.
Das Traurige daran ist, dass dabei die Ecken des Würfels keine sinnvoll nutzbaren Daten enthalten, weil sie Abstände haben, die nicht in allen Richtungen vom Startpunkt aus in der Hyperkugel liegen. Wenn wir uns das konkret in zwei Dimensionen anschauen, dann ist unser 2-dimensionaler Hyperkubus ein Quadrat und die 2-dimensionale Hyperkugel ist ein Kreis. Die beiden haben als Flächeninhalt $ \pi r^2 $ und $ 4 r^2 $. Das Verhältnis von gesammelter und nutzbarer Information ist also $ \pi / 4 \approx 79 \% $. Betrachten wir drei Dimensionen, also eine Kugel und einen Würfel, so erhalten wir nur noch ungefähr 52 % an Nutzbarkeit der gesamten Information. Und dieser Anteil der nutzbaren Information wird mit höheren Dimensionen immer schlechter.
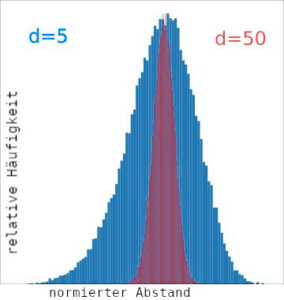Genauer gesagt liegen die Datenpunkte in einem Histogramm der Entfernungen immer enger gedrängt. Die Unterscheidung, ob sich Datenpunkte wirklich ähnlich sind oder nur aufgrund ihrer „Drängung“ nah beieinanderliegen, geht im Rauschen unter. In der Grafik links sind qualitativ die Verteilungen der normierten Abstände bei 5 Dimensionen gegen die Abstände bei 50 Dimensionen dargestellt. In der Praxis kommen Datenmodelle mit Hunderten oder gar Tausenden von Dimensionen vor. Die Grafiken sind einem umfangreicheren Vortrag von DD1AH über dieses Themengebiet entnommen.
Diese „zunehmende Nutzlosigkeit“ hoher Dimensionen wurde vom amerikanischen Mathematiker Richard Ernest Bellman „Fluch der Dimensionalität“ genannt. In der Praxis des Machine Learning hat man genau dieses Problem. Die Lösung davon ist, die Dimensionen mit geeigneten Algorithmen nach Art einer Projektion zu reduzieren. Dies ist gerade ein aktuelles Thema der Forschung. In der englischen Wikipedia gibt es einige Visualisierungen dazu.
Was das umgekehrt für Leute bedeutet, die ohne dieses komplizierte statistische Rüstzeug versuchen, mit dem Ansatz „Viel hilft viel“ aus großen Datenmengen oder big data sinnvolle Informationen zu ziehen, kann sich jeder selbst überlegen. Vergleichbare Probleme entstehen auch beim „technischen Mikromanagement“, wenn versucht wird, mit möglichst viel Betriebsdatenerfassung ganze Unternehmen besonders feingranular zu steuern.
