Bei der Amplitudenmodulation AM wird die NF quasi als Verstärkungsfaktor für die Trägerfrequenz aus unserem Oszilator LO benutzt. Als Formel ausgedrückt ist das ein Produkt. Nehmen wir die NF näherungsweise als einfache Sinus-Schwingung an, sieht das als Formel so aus:
AM = sin(NF) * sin(LO)
Vom perfekten Balance-Mischer wissen wir, dass er die Summe und die Differenz der Mischsignale erzeugt. Tatsächlich ergibt sich aus den Rechenregeln für Sinus und Kosinus dass das das gleiche ist:
AM = 1/2 (cos (NF – LO) – cos (NF + LO))
Lassen wir uns das mit einfachen Zahlen von GnuPlot zeigen:
Damit die Grafiken schön hoch aufgelöst sind, müssen wir als erstes die Anzahl der zu berechnenden Punkte in der Grafik erhöhen:
set samples 10000 plot cos(x - 100*x) - cos(x + 100*x), 2*sin(x)*sin(100*x)+4
Es sieht tatsächlich gleich aus. Wer es genauer wissen will, kann dies unter Additionstheoreme recherchieren.
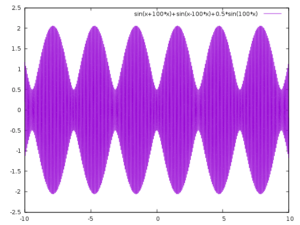
Die Beispiele oben taugen nicht wirklich für die klassische Amplitudenmodulation, denn es fehlt der Träger. Es handelt sich um so genanntes Duales Seitenband DSB. Mit geeigneten Filtern dient DSB als Vorstufe zu SSB. Für AM kann man nun auch einfach den Träger in der Formel hinzufügen.
plot sin(x+100*x)+sin(x-100*x)+0.5*sin(100*x)
Frequenzmodulation
Auch die Frequenzmodulation FM kann man sich mit GnuPlot schön veranschaulichen. Auch hier muss man sich zuerst klar machen, was bei FM mathematisch eigentlich passiert. Hier wird die Frequenz des Trägers mit der NF variiert. Als Formel sieht das so aus:
FM = sin (LO + Hub * sin(NF))
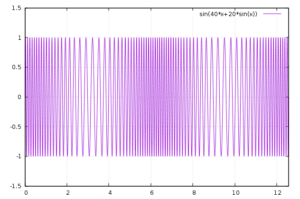
plot sin(40*x + 20*sin(x))
Hier sieht man schön wie die Amplitude konstant bleibt. In ihr wird also keine Information übertragen. Statt dessen sieht man wie die Frequenz schwankt und die Schwingungszüge mal mehr oder mal weniger dicht verlaufen.