Ein SWR ungleich 1 kann durch induktive und kapazitive Lasten entstehen. Umgekehrt kann uns durch diese imaginären Anteile sogar ein niedriges SWR vorgegaukelt werden, obwohl wir keine Resonanz haben. Diesen im wahrsten Sinne des Wortes komplexen Fall betrachten wir hier nicht. Begnügen wir uns hier mit dem resonanten Fall, in dem die Last bekanntlich rein reell ist.
Wenn aus einem TX mit einem Ausgang mit 50 Ω über eine Leitung mit 50 Ω eine Antenne mit 50 Ω angeschlossen ist, dann ist alles bestens. Das SWR ist genau 1 und alles passt. Ob die Antenne die Leistung allerdings wirklich abstrahlt oder im Boden „versenkt“ ist noch mal eine andere Geschichte.
Betrachten wir nun den Fall, dass die Antenne eben nicht 50 Ω hat. Als Erstes muss man hier verstehen, dass HF sich grundsätzlich anders verhält als Gleichstrom. Ernst Lecher hat entdeckt, dass der Spannungsverlauf entlang einer Leitung schwankt. Das passiert immer, wenn die Leitung nicht passend zu ihrer Impedanz abgeschlossen ist. Nur wenn die Impedanz passt, kann die Last die eingespeiste Leistung vollständig aufnehmen.
Bei den mathematisch exakten Extremwerten wird das auch aus den Formeln klar. Ein Kurzschluss lässt zwar den maximalen Strom fließen, hat aber keine Spannung. Und Leistung ist das Produkt aus Spannung und Strom; ohne Spannung gibt es auch keine Leistung. Ein offener Abschluss lässt dagegen keinen Strom fließen. Hier gilt jedoch umgekehrt, dass es ohne Strom keine Leistung gibt, egal bei wie viel Spannung.
Läuft die vorlaufende Leistung jedoch auf einen Lastwiderstand, der nicht ihrer Impedanz entspricht, so stellt sich ein Gleichgewicht ein. Dabei entsteht an der Last eine Spannung, bei der ein Teil der vorlaufenden Leistung an der Last abfällt. Die Differenz dieser Spannung zu der vorlaufenden Spannung läuft als zurücklaufende Spannung zur Quelle zurück. Dabei transportiert sie genau die Differenz zwischen der vorlaufenden Leistung zu der, die an der Last abfällt.
Mit ULast = Uvor + Urück gilt für die Last-Impedanz:
ZLast = (Uvor + Urück) / ILast
Damit die zurücklaufende Leistung negativ zur hin laufenden wird, muss der zurücklaufende Strom negativ sein:
ILast = Ivor – Irück
ZLast = (Uvor + Urück) / (Ivor – Irück)
Damit wir nun eine Aussage über das Verhalten in Abhängigkeit vom Verhältnis von Last-Impedanz zu Quellimpedanz erhalten, teilen wir das durch die Quellimpedanz.
ZLast / ZQuelle= (Uvor + Urück) / (ZQuelle(Ivor – Irück))
Nun ist Quellimpedanz mal I genau die Spannung in die jeweilige Richtung, also:
ZLast / ZQuelle= (Uvor + Urück) / (Uvor – Urück)
Dieses Verhältnis nennen wir das Stehwellenverhältnis. So wie es hier hergeleitet ist, gilt das für die Effektivwerte von Spannung und Strom und wenn die Last-Impedanz größer ist als die Quellimpedanz. Betrachten wir konsequent andere Spannungswerte wie die Spitzenspannung oder die Spitzen-Spitzen-Spannung, gilt die Formel genau so, weil sich der Umrechnungsfaktor kürzen lässt. Nur wenn man mit Leistungen rechnen möchte, sollte man bei den Effektivwerten bleiben. In der Grafik hier sieht man den Anteil der vorlaufenden Spannung, der bei einem bestimmten SWR als zurücklaufende Spannung entsteht. Bei einem SWR von 2 ist es 1/3 und bei einem SWR von 3 die Hälfte.Da die Leistung an konstanter Last quadratisch von der Spannung abhängt und der Faktor hier kleiner als 1 ist, ist der Leistungsfaktor kleiner als der Spannungsfaktor. Konkret ist bei einem SWR von 3 also ein Viertel der Leistung, die bei der Abstrahlung verloren geht. Bedenkt man nun noch, dass wir die Leistung üblicherweise logarithmiert betrachten, so wird einem klar, dass der Verlust an abgestrahlter Leistung durch das SWR in der Praxis eine eher unwichtige Größe ist.
Beachte in obiger Grafik dass auf der y-Achse der Anteil als Faktor angegeben ist. 0,5 bedeutet also 50%.
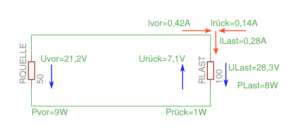Nehmen wir als konkretes Beispiel eine vorlaufende Leistung von 9 W mit 50 Ω Impedanz von Quelle und Kabel. Die Last habe 100 Ω. Das entspricht nach obiger Formel einem SWR von 2. Diese 9 W entsprechen an 50 Ω etwa 21,2 V. Damit würden an 100 Ω aber nur etwa 5 W umgesetzt werden. Nun entsteht eine zurücklaufende Welle mit etwa 7,1V. An der Last liegt genau die Summe von vorlaufender und zurücklaufender Spannung an. Diese 28,3V setzen an 100 Ω jetzt 8W um und die zurücklaufende Welle mit 7,1 V transportiert an 50 Ω genau die Leistungsdifferenz von 1W zurück zur Quelle. In der Grafik sind die Spannungen in Blau eingezeichnet. Eine Masche nach Kirchhoff ergibt, wie zu erwarten 0. Und die Ströme sind in Rot am Knoten oberhalb vom Lastwiderstand eingezeichnet. Auch hier ergibt die Summe wie nach Kirchhoff zu erwarten 0.
Bei einer zu kleinen Last-Impedanz passiert das Ganze umgekehrt. Die Spannung bricht auf einen kleineren Wert zusammen, bis der Gleichgewichtszustand erreicht ist. Hier liegt dann am Lastwiderstand die Differenz zwischen vorlaufender und zurücklaufender Spannung an. In den Formeln vertauschen sich genau die Vorzeichen. Die zurücklaufende Spannung ist negativ, der zurücklaufende Strom positiv, sodass schließlich für ZLast < ZQuelle gilt:
ZQuelle / ZLast = (Uvor + Urück) / (Uvor – Urück)
Die größere Impedanz steht also immer im Zähler. Das SWR ist damit immer >= 1. Ein Punkt, der noch wichtig zu verstehen ist: Wir rechnen hier skalar, haben es uns also eigentlich zu einfach gemacht. Mit den richtigen Vereinfachungen ist das auch zulässig und führt zu den richtigen Ergebnissen. Aber wenn man sich die Verhältnisse z. B. nach Kirchhoff ansieht, entdeckt man schon ein paar Ungereimtheiten. Der Grund ist, dass die Größen eigentlich alle vektoriell zu betrachten sind. In die Strom- und Spannungsrichtung geht nicht nur die Signalrichtung ein, sondern auch die Phasenlage.
Das SWR ist eine passable Methode, um eine Antenne von gut verstandener Funktionsweise abzustimmen. Bei einer unbekannten Last bleiben aber viele Fragen offen. Im Extremfall einer unbekannten komplexen Last kann mir das SWR sogar ein Minimum anzeigen, welches keiner Resonanz entspricht.
Immer wieder kommt auch die Frage auf, wie „schlimm“ denn nun ein schlechtes SWR ist. Die zurücklaufende Leistung verhält sich in der Endstufe wie Verlustleistung. Und die Spannung auf dem Kabel und in den Steckverbindern ist höher als sie sein müsste. Abgesehen davon fehlt die zurücklaufende Leistung natürlich bei der abgestrahlten Leistung. Die Leistung geht quadratisch mit der Spannung. Bei einem SWR von 2 fehlt also mit den Werten von oben 1/9 (~11 %) der Leistung und bei einem SWR von 3 ein Viertel, also beim Empfänger im S-Meter kaum sichtbar.
Netterweise werden VNA so langsam bezahlbar, sodass auch „exotische“ Antennenformen bequem abgestimmt werden können. Aber auch hier immer beachten: Ob die Antenne die Leistung wirklich abstrahlt, ist auch bei perfekter Anpassung nicht automatisch gegeben. Die Leistung kann auch in den Erdströmen verbraucht werden.
