Eine Spule L und ein Kondensator C in Serie sind bei einer bestimmten Frequenz in Resonanz. Bei dieser Frequenz ist die Kombination niederohmig, im perfekten Fall ein Kurzschluss. Man nennt ihn auch Saugkreis, weil er die Energie auf seiner Resonanzfrequenz „absaugt“. Warum ist das so? Und bei welcher Frequenz in Abhängigkeit von L und C ist das so?
Um das genau auszurechnen, kann man die Energie betrachten, die ein Mal als magnetisches Feld in der Spule und ein Mal als elektrisches Feld im Kondensator gespeichert ist. Betrachtet man die beiden als sogenanntes abgeschlossenes System, findet also kein Energieaustausch nach außen statt, so kann man als Lösungsansatz den Energieerhaltungssatz benutzen. Die Summe der Energie in der Spule und der im Kondensator muss immer konstant sein.
Die Rechnung ist länglich und setzt Differenzialgleichungen voraus. Sie ist z. B. in Wikipedia genauer beschrieben. Wir springen hier gleich zur Lösung: Die imaginären Widerstände von Spule und Kondensator müssen für Resonanz in Summe Null ergeben:
XL + XC = 0
Nun gilt:
XL = i ω L
XC = 1/(i ω C)
Das beruht auf den grundlegenden Eigenschaften der Spule, dass die Stromänderung in der Spule der angelegten Spannung proportional ist und die Spannungsänderung am Kondensator dem Strom. Um das auszurechnen, braucht man komplexe Wechselstromrechnung. Wir nehmen das hier einfach als gegeben hin.
Um das i ausklammern zu können, erweitern wir XC mit i. Dieser Teil wird damit negativ, denn das i*i im Nenner ist gleich -1. Nun können wir durch i teilen oder anders gesagt: Wir betrachten hier nur die rein imaginären Anteile und können das i daher konsequent überall weglassen. Das setzen wir nun wieder in die erste Gleichung ein:
ω L – 1/(ω C) = 0
Jetzt bringen wir den Kondensator-Teil auf die rechte Seite, danach das ω in der Gleichung nach links und das L nach rechts. Und so erhalten wir:
ω2 = 1/(LC)
Nun noch die Wurzel ziehen und das ω zu $2 \pi f$ auflösen, $2 \pi$ auf die rechte Seite:
$$ f = \frac {1} {2 \pi \sqrt{LC} } $$
Das ist unsere bekannte Schwingkreisformel, die 1853 von William Thomson formuliert wurde. Die Serienschaltung von L und C ist also bei Resonanzfrequenz rein reell, da der Imaginäranteil von L und C sich genau aufhebt.
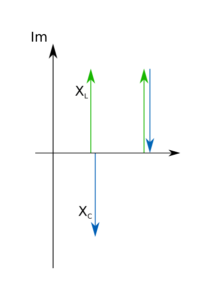Grafisch stellt man so dar, dass der imaginäre Anteil auf der y-Achse dargestellt wird und die x-Achse repräsentiert den reellen Anteil. Hier in der Grafik nutzen wir die reelle Achse nur um Platz zu sparen bzw. um den imaginären Anteil übersichtlicher darzustellen. Mathematisch betrachten wir hier den reellen Anteil nicht.
In der Grafik links sind die imaginären Widerstände unabhängig voneinander eingezeichnet. Wenn die Bauteile in Serie geschaltet sind, hängt man auch die Pfeile ihrer imaginären Widerstände einfach hintereinander, so wie im Bild rechts. Wenn die Spitze des blauen Pfeils vom Kondensator dabei auf der Nulllinie landet, haben wir Resonanz. Ansonsten überwiegt entweder der induktive oder kapazitive Anteil.
Trägt man den Verlauf der resultierenden Pfeilspitze über der Frequenz in dieses Diagramm ein, so erhält man die sogenannte Ortskurve. Das repräsentiert die Veränderung des komplexen Widerstands mit der Frequenz. Das hilft z.B. beim Bewerten und Optimieren von Antennen. Als Messgerät benutzt man dafür einen sogenannten VNA. Solch eine Ortskurve wird auch gern übersichtlich in einem Smith-Diagramm eingezeichnet.
Parallelschwingkreis
Was ist nun anders, wenn Spule und Kondensator parallel geschaltet sind? In Serie addieren sich die Widerstände, parallel addieren sich die Kehrwerte der Widerstände, also die Leitwerte. Die Kehrwerte zweier betragsgleicher Werte sind ebenfalls wieder betragsgleich. Auch die Differenz ist dann also wieder Null. Und ein Leitwert von null bedeutet, dass der Widerstand unendlich ist.
Wie wohl schon bekannt und erwartet, ergibt sich also, dass ein Parallelschwingkreis sich bei der Resonanzfrequenz wie ein Isolator verhält. Man nennt ihn daher auch Sperrkreis. Das wird z. B. in Mehrband-Antennen in den sogenannten Traps benutzt.
