Zwei Funkfreunde verabreden sich zu einem Experiment auf zwei 5km entfernten Berggipfeln im 70cm-Band. Aufgrund des kompakten Aufbaus können Sie die Kabeldämpfung vernachlässigen.
Der eine sendet mit 1W effektiver und isotroper Strahlungsleistung EIRP. Der andere empfängt ihn an einer Antenne ohne Gewinn (0dBi) mit S9+20dB. Das entspricht 50pW Empfangsleistung. Die gesamte Streckendämpfung beträgt also:
Dgesamt = 1W/50pW = 20*109 = 103dB
Die Theorie der Freiraumdämpfung besagt, dass sich die Dämpfung allein aufgrund der Entfernung wie folgt ergibt:
- r = 5km = 5000m
- λ = 70cm = 0,7m
DFreiraum = $ (4 \; \pi \; r / \lambda )^2 = (4 \; \pi \; 5000 / 0,7 ) ^ 2 = 8*10^9 $ = 99dB
Das heißt, bei diesem Experiment wurden zusätzlich 103 – 99 = 4dB Dämpfung aufgrund der Ausbreitungsbedingungen gemessen.
Die wichtige Aussage der Freiraumdämpfung ist, dass schon allein die reine Entfernung ein hohes Maß an Übertragungsdämpfung bewirkt. Besser kann die Übertragung nicht werden. Zu dieser Freiraumdämpfung kommen alle weiteren Einflüsse wie die durch die Atmosphäre noch dazu.
Wer sich etwas in Geometrie auskennt, findet in der Gleichung die Oberfäche einer Kugel. Anschaulich gesagt, verdünnt sich die Sendeleistung mit der Entfernung r auf eine gedachte Kugel mit dem gleichen Radius. Zusätzlich geht noch die Wellenlänge im Nenner mit ein, weil die Antennen linear mit der Wellenlänge größer werden und so einen größeren Anteil der Sendeleistung aus der gedachten Kugel entnehmen.
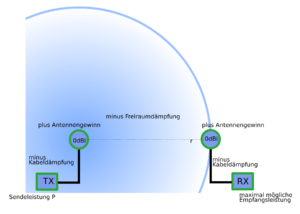
In der Grafik sind alle Größen dargestellt. Wenn man schon die Sendeleistung gleich in dBm angibt, kommt am Ende auch die Empfangsleistung in dBm heraus und man kann das mit der hier verlinkten Tabelle gleich in S-Stufen umrechnen.
Nun kann man sich noch die Frage stellen, wie sich die Freiraumdämpfung relativ mit der Entfernung ändert. Dazu fügen wir in die Gleichung oben einen Faktor 2 bei der Entfernung ein. Durch das Quadrat wird daraus ein Faktor 4. Und wir wissen, dass ein Faktor 2 bei den Dezibel einer Differenz von 3 entspricht. Die Freiraumdämpfung nimmt also bei einer Verdopplung der Entfernung um 6dB zu und die Empfangsleistung nimmt um eine S-Stufe ab. Dass das nicht der praktischen Erfahrung entspricht, liegt daran, dass die Freiraumdämpfung nur einen Teil der gesamten Streckendämpfung ausmacht. Viele weitere Aspekte wie die Erdkrümmung kommen hier noch dazu.
Antennengewinn
Hier noch ein Beispiel wie man das mit Antennengewinn rechnet: Unsere Funkfreunde bauen um: Es wird nur noch mit 1mW, also 0dBm, gesendet und beide benutzen nun Yagis mit 10dB Gewinn gegenüber dem isotropen Strahler (dBi):
0dBm +10dB -103dB +10dB = -83dBm = S9+10dB
30 dB weniger Sendeleistung führen gegenüber den S9+20dB von oben zusammen mit insgesamt 20dB mehr Antennengewinn zu einer Abnahme von 30-20 = 10dB bei der Empfangsleistung. Umgekehrt bedeutet das: Der Antennengewinn muss zur berechneten Dämpfung (hier also 83dB) zwischen Sende- und Empfangsleistung addiert werden um die gesamte Streckendämpfung zu erhalten. Und von der Streckendämpfung zieht man dann die Freiraumdämpfung ab, um die zusätzliche Dämpfung durch die Ausbreitungsbedingungen zu erhalten.
Die vielleicht unerwartete Aussage dass die Freiraumdämpfung von der Frequenz abhängt kommt daher, dass die Empfangsantenne relativ zur Entfernung mit höherer Frequenz immer kleiner wird. Das wird in der Praxis dadurch kompensiert, dass es bei höheren Frequenzen immer leichter wird, Antennen mit hohem Gewinn zu betreiben.
