Strom verlässt nicht so ohne Weiteres seinen Leiter. Und eine Spannung, die aus einer Spannungsquelle an einen Stromkreis angelegt wird, fällt auch in der Schaltung an einem Verbraucher ab. So weit versteht das jeder, der sich mit Elektrik beschäftigt. Etwas komplizierter wird es schon, wenn man die Serien- und Parallelschaltung verstehen will. Aber es gibt Fälle, da hilft einem auch das nicht weiter.
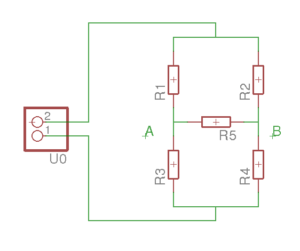 Betrachten wir eine sogenannte Brückenschaltung. Diese Schaltung wird für genaue Messungen und Abgleichaufgaben benutzt. Oft läuft die Messung oder der Abgleich darauf hinaus, dass die Spannung über R5 auf 0 gebracht wird. Dann fließt auch kein Querstrom und man kann R1 einfach in Serie zu R3 betrachten und R2 in Serie zu R4.
Betrachten wir eine sogenannte Brückenschaltung. Diese Schaltung wird für genaue Messungen und Abgleichaufgaben benutzt. Oft läuft die Messung oder der Abgleich darauf hinaus, dass die Spannung über R5 auf 0 gebracht wird. Dann fließt auch kein Querstrom und man kann R1 einfach in Serie zu R3 betrachten und R2 in Serie zu R4.
Wenn man aber mal nicht nur diesen Gleichgewichtszustand betrachten möchte, muss man die Regeln nach Kirchhoff konsequent anwenden.
- An jedem Knoten („Punkt“) ist die Summe aller Ströme (richtungs-richtig gemessen!) gleich 0. „Rein gleich raus.“
- In jeder Masche („geschlossener Stromkreis“) ist in einem Umlauf („Schleife“) die Summe der Spannungen (richtungs-richtig und entlang der Schleife im Kreis gemessen!) gleich 0. Die Masche darf dabei Abzweigungen enthalten.
Als Erstes überlegt man sich, was man eigentlich wissen möchte. In dieser Schaltung wäre z. B. interessant, wie sich der Strom über die Widerstände verteilt. Nennen wir diese Ströme I1 … I5, passend zu den Widerständen, durch die sie fließen. Dann gibt man vor, in welcher Richtung man die Spannungen und Ströme betrachten möchte; sagen wir in diesem Fall von oben nach unten und durch R5 von links nach rechts. Mit der Knotenregel stellen wir die Gleichungen für die Punkte A und B auf:
i1 – i5 – i3 = 0
i2 + i5 – i4 = 0
Letzten Endes möchten wir als Lösung 5 Werte für I1 bis I5 haben. Dafür benötigen wir auch fünf Gleichungen. Also suchen wir noch drei Maschen, in denen auch U0 vorkommen sollte, damit wir ein sinnvolles Ergebnis in Abhängigkeit von der Betriebsspannung erhalten. Hier bedienen wir uns noch des Ohm’schen Gesetzes und beschreiben die Spannung über den Widerständen mit R ∗ I. Beachte, dass die Spannungen einer Masche im Kreis herum betrachtet werden müssen.
u0 – r3*i3 – r1*i1 = 0
u0 – r4*i4 – r2*i2 = 0
u0 – r4*i4 – r5*i5 – r1*i1 = 0
Nun haben wir fünf Gleichungen für fünf gewünschte Lösungen. Solch ein Gleichungssystem zu lösen, ist eine unschöne Fleißaufgabe. Algebra-Software kann hier helfen. Axiom ist ein solches System, welches ähnlich wie Wolfram Alpha arbeitet. Es funktioniert offline und erfordert eine präzisere Syntax:
solve ([i1-i5-i3=0, i2+i5-i4=0, u0-r3*i3-r1*i1=0, u0-r4*i4-r2*i2=0, u0-r4*i4-r5*i5-r1*i1=0 ],[i1,i2,i3,i4,i5])
Die Lösung ist sehr länglich und kompliziert. Als Ergebnis kann man hier zum einen festhalten, dass man es durchaus ausrechnen kann, aber zum anderen wird auch klar, warum man Brückenschaltungen gern im Gleichgewichtszustand betrachtet. 😜
((r4 + r2)r5 + r2 r4 + r2 r3)u0
i1= --------------------------------------------------------------------
((r3 + r1)r4 + r2 r3 + r1 r2)r5 + ((r2 + r1)r3 + r1 r2)r4 + r1 r2 r3
((r3 + r1)r5 + r1 r4 + r1 r3)u0
i2= --------------------------------------------------------------------
((r3 + r1)r4 + r2 r3 + r1 r2)r5 + ((r2 + r1)r3 + r1 r2)r4 + r1 r2 r3
((r4 + r2)r5 + (r2 + r1)r4)u0
i3= --------------------------------------------------------------------
((r3 + r1)r4 + r2 r3 + r1 r2)r5 + ((r2 + r1)r3 + r1 r2)r4 + r1 r2 r3
((r3 + r1)r5 + (r2 + r1)r3)u0
i4= --------------------------------------------------------------------
((r3 + r1)r4 + r2 r3 + r1 r2)r5 + ((r2 + r1)r3 + r1 r2)r4 + r1 r2 r3
(- r1 r4 + r2 r3)u0
i5= --------------------------------------------------------------------
((r3 + r1)r4 + r2 r3 + r1 r2)r5 + ((r2 + r1)r3 + r1 r2)r4 + r1 r2 r3
Die Gleichungen sind ziemlich unübersichtlich, aber eine Sache kann man doch herauslesen: I1 … I4 sind garantiert immer positiv, so lange U0 positiv ist. Nur I5 kann je nach Verhältnis von R1 * R4 zu R2 * R3 auch negativ werden. Wenn man sich die Schaltung noch mal ansieht, wird das auch anschaulich klar. Und alle Ströme hängen direkt linear von U0 ab, was auch wieder anschaulich klar wird. Interessant ist auch, dass der Nenner immer gleich ist. Sollte man das also wirklich mal in Zahlen ausrechnen wollen, wird man diesen ein mal für alle Ströme vorab ausrechnen.
Auch immer sinnvoll ist eine Kontrolle, ob die Einheiten stimmen. Die Einheit vom Zähler ist Ω2 V. Also muss der Nenner Ω3 sein, damit ein Strom herauskommt. Wenn man die Klammern sorgfältig auflöst, stellt man fest, dass das der Fall ist. Das passt also auch.
Hier auch noch die Syntax für Wolfram Alpha. Das i würde hier als imaginäre Einheit interpretiert. Daher benutzen wir das j.
solve (j1 - j5 - j3 = 0 , j2 + j5 - j4 = 0, u0 - r3*j3 - r1*j1 = 0, u0 - r4*j4 - r2*j2 = 0, u0 - r4*j4 - r5*j5 - r1*j1= 0 ) for j1, j2, j3, j4, j5
Ein anderes schönes Tool für das symbolische Rechnen ist GNU Octave. Es ähnelt mehr einer Programmiersprache. Damit lassen sich dann auch kompliziertere Dinge ausrechnen. Dafür lassen sich aber umgekehrt auch solche Aufgaben wie hier dann nicht mehr als Einzeiler schreiben:
pkg load symbolic syms i1 i2 i3 i4 i5 u0 r1 r2 r3 r4 r5 solve (i1-i5-i3==0, i2+i5-i4==0, u0-r3*i3-r1*i1==0, u0-r4*i4-r2*i2==0, u0-r4*i4-r5*i5-r1*i1==0,i1,i2,i3,i4,i5)